Satellite knot

In the mathematical theory of knots, a satellite knot is a knot that contains an incompressible, non-boundary parallel torus in its complement.^[1] The class of satellite knots include composite knots, cable knots and Whitehead doubles. (See Basic families, below for definitions of the last two classes.)

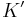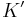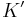A satellite knot $K$ can be picturesquely described as follows: start by taking a nontrivial knot $K'$ lying inside an unknotted solid torus $V$ . Here "nontrivial" means that the knot $K'$ is not allowed to sit inside of a 3-ball in $V$ and $K'$ is not allowed to be isotopic to the central core curve of the solid torus. Then tie up the solid torus into a nontrivial knot. This means there is a non-trivial embedding 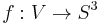$f:V \to S^3$ and $K=f(K')$ . 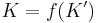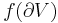The central core curve of the solid torus $V$ is sent to a knot $H$ , which is called the "companion knot" and is thought of as the planet around which the "satellite knot" $K$ orbits.The construction ensures that $f(\partial V)$ is a non-boundary parallel incompressible torus in the complement of $K$ . Composite knots contain a certain kind of incompressible torus called a swallow-follow torus, which can be visualized as swallowing one summand and following another summand.

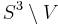Since $V$ is an unknotted solid torus, $S^3 \setminus V$ is a tubular neighbourhood of an unknot 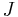$J$ . The 2-component link $K' \cup J$ together with the embedding $f$ is called the pattern associated to the satellite operation.

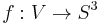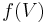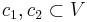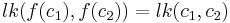A convention: people usually demand that the embedding $f�: V \to S^3$ is untwisted in the sense that $f$ must send the standard longitude of $V$ to the standard longitude of $f(V)$ . Said another way, given two disjoint curves $c_1,c_2 \subset V$ , $f$ must preserve their linking numbers i.e.: $lk(f(c_1),f(c_2))=lk(c_1,c_2)$ .

1 Basic families
2 Examples
3 Origins
4 Follow-up work
5 Uniqueness of satellite decomposition
6 References

Basic families

When 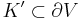$K' \subset \partial V$ is a torus knot, then $K$ is called a cable knot. Examples 3 and 4 are cable knots.

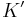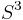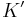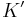If $K'$ is a non-trivial knot in $S^3$ and if a compressing disc for $V$ intersects $K'$ in precisely one point, then $K$ is called a connect-sum. Another way to say this is that the pattern $K' \cup J$ is the connect-sum of a non-trivial knot $K'$ with a Hopf link.

If the link $K' \cup J$ is the Whitehead link, $K$ is called a Whitehead double. If $f$ is untwisted, $K$ is called an untwisted Whitehead double.

Examples

Example 1: The connect-sum of a figure-8 knot and trefoil.

Example 2: Untwisted Whitehead double of a figure-8.

Example 3: Cable of a connect-sum.

Example 4: Cable of trefoil.

Examples 5 and 6 are variants on the same construction. They both have two non-parallel, non-boundary-parallel incompressible tori in their complements, splitting the complement into the union of three manifolds. In Example 5 those manifolds are: the Borromean rings complement, trefoil complement and figure-8 complement. In Example 6 the figure-8 complement is replaced by another trefoil complement.

Origins

In 1949 ^[2] Horst Schubert proved that every oriented knot in 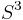$S^3$ decomposes as a connect-sum of prime knots in a unique way, up to reordering, making the monoid of oriented isotopy-classes of knots in 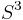$S^3$ a free commutative monoid on countably-infinite many generators. Shortly after, he realized he could give a new proof of his theorem by a close analysis of the incompressible tori present in the complement of a connect-sum. This led him to study general incompressible tori in knot complements in his epic work Knoten und Vollringe,^[3] where he defined satellite and companion knots.

Follow-up work

Schubert's demonstration that incompressible tori play a major role in knot theory was one several early insights leading to the unification of 3-manifold theory and knot theory. It attracted Waldhausen's attention, who later used incompressible surfaces to show that a large class of 3-manifolds are homeomorphic if and only if their fundamental groups are isomorphic.^[4] Waldhausen conjectured what is now the Jaco–Shalen–Johannson-decomposition of 3-manifolds, which is a decomposition of 3-manifolds along spheres and incompressible tori. This later became a major ingredient in the development of geometrization, which can be seen as a partial-classification of 3-dimensional manifolds. The ramifications for knot theory were first described in the long-unpublished manuscript of Bonahon and Siebenmann.^[5]

Uniqueness of satellite decomposition

In Knoten und Vollringe, Schubert proved that in some cases, there is essentially a unique way to express a knot as a satellite. But there are also many known examples where the decomposition is not unique.^[6] With a suitably enhanced notion of satellite operation called splicing, the JSJ decomposition gives a proper uniqueness theorem for satellite knots.^[7]^[8]

References

^ Colin Adams, The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots, (2001), ISBN 0-7167-4219-5
^ Schubert, H. Die eindeutige Zerlegbarkeit eines Knotens in Primknoten. S.-B Heidelberger Akad. Wiss. Math.-Nat. Kl. 1949 (1949), 57–104.
^ Schubert, H. Knoten und Vollringe. Acta Math. 90 (1953), 131–286.
^ Waldhausen, F. On irreducible 3-manifolds which are sufficiently large.Ann. of Math. (2) 87 (1968), 56–88.
^ F.Bonahon, L.Siebenmann, New Geometric Splittings of Classical Knots, and the Classification and Symmetries of Arborescent Knots, [1]
^ Motegi, K. Knot Types of Satellite Knots and Twisted Knots. Lectures at Knots '96. World Scientific.
^ Eisenbud, D. Neumann, W. Three-dimensional link theory and invariants of plane curve singularities. Ann. of Math. Stud. 110
^ Budney, R. JSJ-decompositions of knot and link complements in S^3. L'enseignement Mathematique 2e Serie Tome 52 Fasc. 3–4 (2006). arXiv:math.GT/0506523